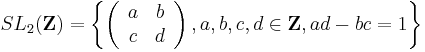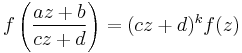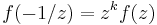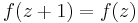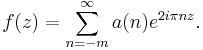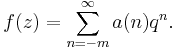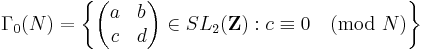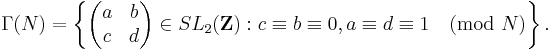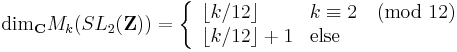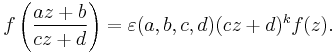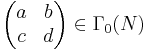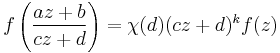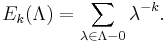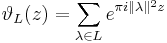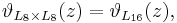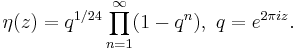Modular form

In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology and string theory.

A modular function is a modular form, without the condition that f(z) be holomorphic at infinity. Instead, modular functions are meromorphic at infinity.

Modular form theory is a special case of the more general theory of automorphic forms, and therefore can now be seen as just the most concrete part of a rich theory of discrete groups.

1 Modular forms for SL₂(Z)
- 1.1 Definition in terms of lattices or elliptic curves
- 1.2 Modular functions
2 Modular forms for more general groups
3 Misc
- 3.1 Entire forms
- 3.2 Automorphic factors and other generalizations
4 Examples
5 Generalizations
6 History
7 Notes
8 References

Modular forms for SL₂(Z)

A modular form of weight k for the group

$SL_2(\mathbf Z) = \left \{ \left ( \begin{array}{cc}a & b \\ c & d \end{array} \right ), a, b, c, d \in \mathbf Z, ad-bc = 1 \right \}$

is a complex-valued function f on H = {z ∈ C, Im(z) > 0}, satisfying the following three conditions: firstly, f is a holomorphic function on H. Secondly, for any z in H and any matrix in SL₂(Z) as above, the equation

$f\left(\frac{az%2Bb}{cz%2Bd}\right) = (cz%2Bd)^k f(z)$

is required to hold. Thirdly, f is required to be holomorphic as 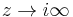$z\rightarrow i\infty$ . The latter condition is also phrased by saying that f is "holomorphic at the cusp", a terminology that is explained below. The weight k is typically a positive integer.

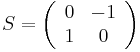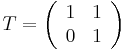The second condition, with the matrices $S = \left ( \begin{array}{cc}0 & -1 \\ 1 & 0 \end{array} \right )$ and $T = \left ( \begin{array}{cc}1 & 1 \\ 0 & 1 \end{array} \right )$ reads

$f(-1/z) = z^k f(z)\,$

and

$f(z%2B1) = f(z)\,$

respectively. Since S and T generate the modular group SL₂(Z), the second condition above is equivalent to these two equations.

Definition in terms of lattices or elliptic curves

A modular form can equivalently be defined as a function F from the set of lattices Λ in C (that is, subgroups of C that are isomorphic to Z²) to the set of complex numbers which satisfies certain conditions:

(1) If we consider the lattice 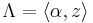$\Lambda = \langle \alpha, z\rangle$ generated by a constant α and a variable z, then F(Λ) is an analytic function of z.

(2) If α is a non-zero complex number and αΛ is the lattice obtained by multiplying each element of Λ by α, then F(αΛ) = α^−kF(Λ) where k is a constant (typically a positive integer) called the weight of the form.

(3) The absolute value of F(Λ) remains bounded above as long as the absolute value of the smallest non-zero element in Λ is bounded away from 0.

The key idea in proving the equivalence of the two definitions is that such a function F is determined, because of the first property, by its values on lattices of the form 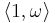$\langle 1, \omega \rangle$ , where ω ∈ H.

Modular functions

When the weight k is zero, the only modular forms are constant functions, as can be shown. However, relaxing the requirement that f be holomorphic leads to the notion of modular functions. A function f : H → C is called modular iff it satisfies the following properties:

f is meromorphic in the open upper half-plane H.
For every matrix M in the modular group Γ, f(Mτ) = f(τ).
f is required to be "meromorphic at the cusp". This means the following: as pointed out above, the second condition implies that f is periodic, and therefore has a Fourier series. The third condition is that this series is of the form

$f(z) = \sum_{n=-m}^\infty a(n) e^{2i\pi nz}.$

It is often written in terms of as 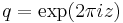$q=\exp(2\pi i z)$ (the square of the nome),

$f(z)=\sum_{n=-m}^\infty a(n) q^n.$

This is also referred to as the q-expansion^[1] of f (see also q-analog). The coefficients a(n) are known as the Fourier coefficients of f, the number m is called the order of the pole of f at 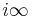$i\infty$ .

Another way to phrase the definition of modular functions is to use elliptic curves: every lattice Λ determines an elliptic curve C/Λ over C; two lattices determine isomorphic elliptic curves if and only if one is obtained from the other by multiplying by some non-zero complex number α. Thus, a modular function can also be regarded as a meromorphic function on the set of isomorphism classes of elliptic curves. For example, the j-invariant j(z) of an elliptic curve, regarded as a function on the set of all elliptic curves, is a modular function. More conceptually, modular functions can be thought of as functions on the moduli space of isomorphism classes of complex elliptic curves.

A modular form f that vanishes at 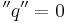$''q''=0$ (equivalently, a(0) = 0, also paraphrased as z = i∞) is called a cusp form (Spitzenform in German). The smallest n such that a(n) ≠ 0 is the order of the zero of f at i∞.

Modular forms for more general groups

The functional equation, i.e., the behavior of f with respect to z ↦ (az + b)/(cz + d) can be relaxed by requiring it only for matrices in smaller groups.

The Riemann surface G\H^∗

Let G be a subgroup of SL(2, Z) that is of finite index. Such a group G acts on H in the same way as SL(2, Z). The quotient topological space G\H can be shown to be a Hausdorff space. Typically it is not compact, but can be compactified by adding a finite number of points called cusps. These are points at the boundary of H, i.e., either in Q, the rationals, or ∞, such that there is a parabolic element of G (a matrix with trace ±2) fixing the point. Here, a matrix 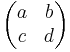$\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ sends ∞ to a/c. This yields a compact topological space G\H^∗. What is more, it can be endowed with the structure of a Riemann surface, which allows to speak of holo- and meromorphic functions.

Important examples are, for any positive integer N, either one of the congruence subgroups

$\Gamma_0(N) = \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in SL_2(\mathbf{Z})�: c \equiv 0 \pmod{N} \right\}$

and

$\Gamma(N) = \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in SL_2(\mathbf{Z})�: c \equiv b \equiv 0, a \equiv d \equiv 1 \pmod{N} \right\}.$

For G = Γ0(N) or Γ(N), the spaces G\H and G\H^∗ are denoted Y₀(N) and X₀(N) and Y(N), X(N), respectively.

The geometry of G\H^∗ can be understood by studying fundamental domains for G, i.e. subsets D ⊂ H such that D intersects each orbit of the G-action on H exactly once and such that the closure of D meets all orbits. For example, the genus of G\H^∗ can be computed.^[2]

Definition

A modular form for G of weight k is a function on H satisfying the above functional equation for all matrices in G, that is holomorphic on H and at all cusps of G. Again, modular forms that vanish at all cusps are called cusp forms for G. The C-vector spaces of modular and cusp forms of weight k are denoted M_k(G) and S_k(G), respectively. Similarly, a meromorphic function on G\H^∗ is called a modular function for G. In case G = Γ₀(N), they are also referred to as modular/cusp forms and functions of level N. For G = Γ(1) = SL₂(Z), this gives back the afore-mentioned definitions.

Consequences

The theory of Riemann surfaces can be applied to G\H^∗ to obtain further information about modular forms and functions. For example, the spaces M_k(G) and S_k(G) are finite-dimensional, and their dimensions can be computed thanks to the Riemann-Roch theorem in terms of the geometry of the G-action on H.^[3] For example,

$\text{dim}_{\mathbf C} M_k(SL_2(\mathbf Z)) = \left \{ \begin{array}{ll} \lfloor k/12 \rfloor & k \equiv 2 \pmod{12} \\ \lfloor k/12 \rfloor %2B 1 & \text{else} \end{array} \right.$

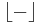where $\lfloor - \rfloor$ denotes the floor function.

The modular functions constitute the field of functions of the Riemann surface, and hence form a field of transcendence degree one (over C). If a modular function f is not identically 0, then it can be shown that the number of zeroes of f is equal to the number of poles of f in the closure of the fundamental region R_Γ.It can be shown that the field of modular function of level N (N ≥ 1) is generated by the functions j(z) and j(Nz).^[4]

Line bundles

The situation can be profitably compared to that which arises in the search for functions on the projective space P(V): in that setting, one would ideally like functions F on the vector space V which are polynomial in the coordinates of v≠ 0 in V and satisfy the equation F(cv) = F(v) for all non-zero c. Unfortunately, the only such functions are constants. If we allow denominators (rational functions instead of polynomials), we can let F be the ratio of two homogeneous polynomials of the same degree. Alternatively, we can stick with polynomials and loosen the dependence on c, letting F(cv) = c^kF(v). The solutions are then the homogeneous polynomials of degree k. On the one hand, these form a finite dimensional vector space for each k, and on the other, if we let k vary, we can find the numerators and denominators for constructing all the rational functions which are really functions on the underlying projective space P(V).

One might ask, since the homogeneous polynomials are not really functions on P(V), what are they, geometrically speaking? The algebro-geometric answer is that they are sections of a sheaf (one could also say a line bundle in this case). The situation with modular forms is precisely analogous.

Modular forms can also be profitably approached from this geometric direction, as sections of line bundles on the moduli space of elliptic curves.

Misc

Entire forms

If f is holomorphic at the cusp (has no pole at 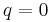$q=0$ ), it is called an entire modular form.

If f is meromorphic but not holomorphic at the cusp, it is called a non-entire modular form. For example, the j-invariant is a non-entire modular form of weight 0, and has a simple pole at 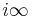$i\infty$ .

Automorphic factors and other generalizations

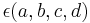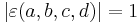Other common generalizations allow the weight k to not be an integer, and allow a multiplier $\epsilon(a,b,c,d)$ with $\left|\varepsilon(a,b,c,d)\right|=1$ to appear in the transformation, so that

$f\left(\frac{az%2Bb}{cz%2Bd}\right) = \varepsilon(a,b,c,d) (cz%2Bd)^k f(z).$

Functions of the form 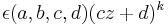$\epsilon(a,b,c,d) (cz%2Bd)^k$ are known as automorphic factors.

By allowing automorphic factors, functions such as the Dedekind eta function may be encompassed by the theory, being a modular form of weight 1/2. Thus, for example, let 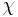$\chi$ be a Dirichlet character mod N. A modular form of weight k, level N (or level group 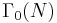$\Gamma_0(N)$ ) with nebentypus the Dirichlet character 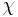$\chi$ is a holomorphic function f on the upper half-plane such that for any

$\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma_0(N)$

and any z in the upper half-plane, we have

$f\left(\frac{az%2Bb}{cz%2Bd}\right) = \chi(d)(cz%2Bd)^k f(z)$

and f is holomorphic at all the cusps; when the form vanishes at all cusps, it is called a cusp form.

Examples

The simplest examples from this point of view are the Eisenstein series. For each even integer k > 2, we define E_k(Λ) to be the sum of λ^−k over all non-zero vectors λ of Λ:

$E_k(\Lambda) = \sum_{\lambda\in\Lambda-0}\lambda^{-k}.$

The condition k > 2 is needed for convergence; the condition that k is even prevents λ^−k from cancelling with (−λ)^−k.

An even unimodular lattice L in Rⁿ is a lattice generated by n vectors forming the columns of a matrix of determinant 1 and satisfying the condition that the square of the length of each vector in L is an even integer. As a consequence of the Poisson summation formula, the theta function

$\vartheta_L(z) = \sum_{\lambda\in L}e^{\pi i \Vert\lambda\Vert^2 z}$

is a modular form of weight n/2. It is not so easy to construct even unimodular lattices, but here is one way: Let n be an integer divisible by 8 and consider all vectors v in Rⁿ such that 2v has integer coordinates, either all even or all odd, and such that the sum of the coordinates of v is an even integer. We call this lattice L_n. When n=8, this is the lattice generated by the roots in the root system called E₈. Because there is only one modular form of weight 8 up to scalar multiplication,

$\vartheta_{L_8\times L_8}(z) = \vartheta_{L_{16}}(z),$

even though the lattices L₈×L₈ and L₁₆ are not similar. John Milnor observed that the 16-dimensional tori obtained by dividing R¹⁶ by these two lattices are consequently examples of compact Riemannian manifolds which are isospectral but not isometric (see Hearing the shape of a drum.)

The Dedekind eta function is defined as

$\eta(z) = q^{1/24}\prod_{n=1}^\infty (1-q^n),\ q = e^{2\pi i z}.$

Then the modular discriminant Δ(z)=η(z)²⁴ is a modular form of weight 12. The presence of 24 can be connected to the Leech lattice, which has 24 dimensions. A celebrated conjecture of Ramanujan asserted that the q^p coefficient for any prime p has absolute value ≤2p^11/2. This was settled by Pierre Deligne as a result of his work on the Weil conjectures.

The second and third examples give some hint of the connection between modular forms and classical questions in number theory, such as representation of integers by quadratic forms and the partition function. The crucial conceptual link between modular forms and number theory are furnished by the theory of Hecke operators, which also gives the link between the theory of modular forms and representation theory.

Generalizations

There are a number of other usages of the term modular function, apart from this classical one; for example, in the theory of Haar measures, it is a function Δ(g) determined by the conjugation action.

Maass forms are real-analytic eigenfunctions of the Laplacian but need not be holomorphic. The holomorphic parts of certain weak Maass wave forms turn out to be essentially Ramanujan's mock theta functions. Groups which are not subgroups of SL(2,Z) can be considered.

Hilbert modular forms are functions in n variables, each a complex number in the upper half-plane, satisfying a modular relation for 2×2 matrices with entries in a totally real number field.

Siegel modular forms are associated to larger symplectic groups in the same way in which the forms we have discussed are associated to SL(2,R); in other words, they are related to abelian varieties in the same sense that our forms (which are sometimes called elliptic modular forms to emphasize the point) are related to elliptic curves.

Jacobi forms are a mixture of modular forms and elliptic functions. Examples of such functions are very classical - the Jacobi theta functions and the Fourier coefficients of Siegel modular forms of genus two - but it is a relatively recent observation that the Jacobi forms have an arithmetic theory very analogous to the usual theory of modular forms.

Automorphic forms extend the notion of modular forms to general Lie groups.

History

The theory of modular forms was developed in three or four periods: first in connection with the theory of elliptic functions, in the first part of the nineteenth century; then by Felix Klein and others towards the end of the nineteenth century as the automorphic form concept became understood (for one variable); then by Erich Hecke from about 1925; and then in the 1960s, as the needs of number theory and the formulation of the modularity theorem in particular made it clear that modular forms are deeply implicated.

The term modular form, as a systematic description, is usually attributed to Hecke.

Notes

^ Elliptic and Modular Functions
^ Gunning, Robert C. (1962), Lectures on modular forms, Annals of Mathematics Studies, 48, Princeton University Press , p. 13
^ Shimura, Goro (1971), Introduction to the arithmetic theory of automorphic functions, Publications of the Mathematical Society of Japan, 11, Tokyo: Iwanami Shoten , Theorem 2.33, Proposition 2.26
^ Milne, James (2010), Modular Functions and Modular Forms, http://www.jmilne.org/math/CourseNotes/MF.pdf , Theorem 6.1.

References

Jean-Pierre Serre: A Course in Arithmetic. Graduate Texts in Mathematics 7, Springer-Verlag, New York, 1973. Chapter VII provides an elementary introduction to the theory of modular forms.
Tom M. Apostol, Modular functions and Dirichlet Series in Number Theory (1990), Springer-Verlag, New York. ISBN 0-387-97127-0
Goro Shimura: Introduction to the arithmetic theory of automorphic functions. Princeton University Press, Princeton, N.J., 1971. Provides a more advanced treatment.
Stephen Gelbart: Automorphic forms on adele groups. Annals of Mathematics Studies 83, Princeton University Press, Princeton, N.J., 1975. Provides an introduction to modular forms from the point of view of representation theory.
Robert A. Rankin, Modular forms and functions, (1977) Cambridge University Press, Cambridge. ISBN 0-521-21212-X
Stein's notes on Ribet's course Modular Forms and Hecke Operators
Erich Hecke: "Mathematische Werke" , Goettingen, Vandenhoeck & Ruprecht, 1970.
NP Skoruppa, D Zagier Jacobi forms and a certain space of modular forms, Inventiones Mathematicae, 1988, Springer